A becsület foltjai és rendje – Gaspard Monge (1746–1818)
Gaspard Monge neve azok fülében is biztatóan cseng, akiknek egy jobb általános iskolában módjukban állt az ábrázoló geometria alapjaival megismerkedni. Akárhogy is, sokak számára jellegzetes „ismeretlen ismerős”, mint sokan a reáltudományok nagyjai közül, akik életútjának bemutatásával az utókor, ismeretlen okból, mostohább, mint művészekével vagy filozófusokéval. Pedig éppen az a célom, hogy megvilágítsam, egy-egy ilyen életmű szintén a legszorosabb kapcsolatban áll a megalkotója felfogásával, világnézetével és rejtettebb magánéletével – és ez olykor, amikor az életmű kimondottan gazdag, különös jelentőségre tesz szert. Monge-é éppen ilyen eset.

Georg Wilhelm Friedrich Hegel (1770–1831) 1989-ben bizonyára megállapította volna, hogy a világszellem elfordult a francia forradalomtól. A korábban doktriner baloldali történész, François Furet (1927–1997) már 1981-ben úgy ítélte, a francia forradalomnak vége van (A francia forradalom értelmezése című monográfiájában), értelemszerűen nemcsak a forradalmi naptárban, hanem a szívekben és az elmékben is. 1989-re egykori álláspontját is revideálta. Korábban úgy tartotta, 1793 volt a fordulópont, a vállalhatatlanság kezdete. A kétszázadik évfordulón már ott járt, hogy a terror már az 1789-es eseményekbe bele volt kódolva, azok egyenes ági következménye volt. Egy fecske nem csinál nyarat? A népszerű francia történész nem volt egyedül a véleményével. Egy francia közvélemény-kutatás résztvevői sem „ültek fel” a csábító „ott és akkor erre volt szükség” formulájának. 64%-uk a terrort a francia forradalom szégyenfoltjának minősítette. Ha ebbe a széles körben megmutatkozó hangulatba bele is játszhatott az akkor létező baloldali világrend végválsága, nem mindenki adta át magát az uralkodó érzésnek. A köztársasági elnök, François (Maurice Adrien Marie) Mitterrand (1916–1996) nemcsak nagyszabású – és ezért bírált – megemlékezéssorozatot szervezett a kétszázadik évfordulóra, de forradalompárti nézeteit alku nélkül meg is védelmezte. Hogy a személyes meggyőződésén túl aktuálpolitikusi ügyesség is szerephez jutott-e bölcs döntésében, nehéz lenne kideríteni: kiválasztotta a forradalmi idők három feddhetetlen – vagy szinte feddhetetlen – alakját, és őket helyezte az ünnepség középpontjába. Ez a három személyiség a színesbőrűek emberi mivoltáért és jogaiért kiálló, ugyanakkor a született előjogok ellen küzdő Henri Jean-Baptiste Grégoire (1750–1831) abbé; a matematikus és humanista filozófus Marie Jean Antoine Nicolas Caritat (1743–1794), azaz Condorcet márkija, akinek sok értékes gondolata volt a választási rendszerekről is; végül pedig a matematikus-polihisztor Gaspard Monge, aki 1746. május 10-én, 275 évvel ezelőtt született. (Condorcet márkit a forradalom idején tömegsírba temették, a másik két nagyság földi maradványait átszállították a Pantheonba.)
Monge élete
Monge a burgund borvidék fővárosában, Beaune-ban született, kimondottan alacsony sorban. Anyja, Jeanne Rousseau-Monge (1711–1773) egy városi teherszállító lánya volt, apja, Jacques Monge (1718–1775) köszörűs és házaló. Gaspard volt az elsőszülött. Noha a család anyagi körülményei szűkösek voltak, apja különös súlyt helyezett a gyerekek, Gaspard, Louis (1748–1827) és Jean (1751–1813) neveltetésére és taníttatására. Az „Isten bohóca”, „Róma második apostola”, Néri Szent Fülöp (1515–1595) által 1565-ben alapított világi papi kongregáció, az oratoriánusok („imádkozóhelyen gyülekezők”) helyi kollégiumába adta a három fivért. Ott elemi és középiskolai tanulmányaikat valamennyien kitűnő eredménnyel végezték. A fivérek közül mégis Gaspard mutatott fel kiemelkedő képességeket. Tizenhatodik éve betöltésével filozófiai-matematikai-fizikai „szakképesítésre” tett szert. Tanulmányait a rend Szentháromságról nevezett lyoni kollégiumában folytatta, ahol két évre rá már fizikát oktatott – ne felejtsük, az ancien régime-ben, amikor az életkor alapú tiszteletadás jellemző volt. Az eskütételi kötelezettség nélküli rendi szabályokat sem kívánta magára venni, így visszautasította az atyák meghívását. Beaune-ba hazaérve egy ideig munka nélkül élt, de amikor a szülővárosáról maga alkotta földmérő eszközökkel és projekciós módszerrel szerkesztett részletes térképe Vigneaux gárdaalezredes kezébe került, aki Mézières-ben, az 1748-ban alapított, nagy tekintélyű École Royale de Génie, Királyi Elitképző Iskola (hadmérnöki felsőfokú tanintézet) második embere volt, meghívást kapott az intézetbe, szerény családi háttere miatt azonban csak technikusi állást kaphatott. Feladata erődök tervezése, épületmodellek készítése volt. A geometriai ábrázolás akkoriban „gyerekcipőben járt”. A fő vonalak megszerkesztését követően a képet a tárgy közelebbi tanulmányozása után véglegesítették. Monge kiváló térlátással a vetítés módszerét megbízható tudományos alapokra helyezte. Módszere, a két merőleges síkra történő vetítés kiválóan láttató megoldása (a síkokat elválasztó nevezetes X1-2 tengellyel) lett az alapja minden kétséget kizáróan legemlékezetesebb művének, az ábrázoló geometriának, mely a nála csekélyebb térlátási képességűek számára is megkönnyíti tárgyak felismerését és egymáshoz képesti térbeli viszonyaik, például áthatásaik megjelenítését. Kiforrott módszere ma, a számítógépes korban is a mérnöki tanulmányok fontos (ha nem is egyöntetűen élvezett) fejezete, melynek elsajátítása nélkül a térlátás kifejlesztése azokban, akiknek ez nem veleszületett képessége, jószerével reménytelen. Magas szintű programozási technikával, például POV-Ray alkalmazásával a felhasználó természetesen elkerülheti Monge elveinek megismerését, de a programnyelvek megalkotói számára ez nem megkerülhető. Monge munkája, a Géométrie descriptive, Ábrázoló geometria első kiadása 1795-re öltött „testet”.
A matematika tanszéket vezető Charles Bossut (1730–1814) abbé, maga is kora jeles matematikusa, aki a jezsuitáknál nevelkedett, és akinek pályáját a legnagyobbak közé sorolható Jean Le Rond d’Alembert (1717–1783) és Alexis Claude Clairaut (1713–1765) egyengették, csakhamar felfigyelt a kiemelkedő képességű technikusra. Bossut tanítványai közé tartozott Jean Charles de Borda (1733–1799) és Charles Augustin de Coulomb (1736–1806). Bossut Monge-ot gyakorlatvezetőjévé, majd vizsgáztatóvá emelte, és rövidesen, 1769-ben a tanszékvezetői posztot is átadta neki, aki huszonöt éves fejjel, érthetően, nem volt még professzor. (Ehhez társult 1790-ben a fizika tanszék vezetése is.) 1777-ben Monge feleségül vette egy vasgyáros özvegyét, Marie-Catherine Huart-t (1747–1846). A Monge családba három lánygyermek született, akik közül ketten érték meg a felnőttkort.
Mivel hozományként megkapta a kicsiny gyárat is, érdeklődése a fémek technológiájára is kezdett kiterjedni. Ennek tudományos eredménye tükröződik az Alexandre-Théophile Vandermonde-dal (1735–1796), a neves matematikussal, hegedűművésszel és vegyésszel, valamint Claude Louis Berthollet (1748–1822) kiemelkedő vegyésszel 1786-ban írt tanulmányában a vas különböző fázisállapotairól. A Francia Tudományos Akadémiának ebben az időszakban ahhoz hasonló fokozatai voltak, mint ma az egyetemeknek. Mikor Vandermonde-ot associévé (kb. docenssé) nevezték ki, a megüresedett adjoint (kb. adjunktus) posztot 1780 áprilisában Monge-nak kínálták fel. A kinevezés azzal járt, hogy az év öt hónapját Párizsban kellett töltenie. Egy ilyen adottságú családban ez nem jelenthet problémát: ilyenkor Mézières-ben öccse, a szintén műszaki képzésben részesült Louis helyettesítette. Jelentett azonban problémát, konfliktust – érthetően – magával a zseniképzővel.
1775-ben Anne Robert Jacques Turgot (1727–1781), L’Aulne bárója hidraulikai tanszéket alapított nem kisebb patinájú helyen, mint a Louvre-ban. Vezetőjévé Bossut-t nevezték ki. Vélhetőleg a Monge és a Mézières-i iskola között kirobbant konfliktus elegyengetésére Monge magas pártfogója, Charles Eugène Gabriel de La Croix (1727–1801), Castries márkija, flottaügyi miniszter az akkor adjunktus Monge-ot ugyanebben a posztban visszahelyezte Bossut alá. A kinevezési folyamodványt XVI. Lajos (1754–1793) szignálta dicséretes tömörséggel: „Bon” („Jó”). Monge kapcsolata azonban 1784-ig nem szakadt meg korábbi munkahelyével, az elit iskolával. Ez csak akkor következett be, amikor a nagy algebrista, Étienne Bézout (1730–1783) halálával Monge-t nevezték ki helyére a következő évtől a flotta vizsgáztató tanárának. 1785-ben az Akadémián Monge-ból automatikusan associé lett azok után, hogy az adjoint fokozatot eltörölték. 1786-ban a haarlemi Holland Tudományos Társaság a tagjai közé választotta.
Az ancien régime, ezen belül a Premier Ordre láthatólag a tenyerén hordozta Monge-ot, aki származási hátrányát tehetségével ellensúlyozva szerzett presztízst magának. A kegy azonban a legkevésbé sem befolyásolta Monge véleményét kora társadalmi berendezkedéséről. A francia forradalmat nemcsak üdvözölte, de fokozatosan radikalizálódott is: eljutott odáig, hogy csatlakozott a Jakobinus klubhoz. A tisztelet kölcsönös volt: 1792-ben a végrehajtó tanács őt nevezte ki flottaügyi miniszterré. Kevesebb mint egy éven át viselte a hivatalt. Nélküle is lefejezték volna XVI. Lajost, semmi kétség. De Monge hivatalból a nevét adta a döntéshez, ő volt a halálos ítélet hat aláírójának egyike.
1793-tól a Konvent nagy arányú iskolabezárásokat foganatosított. Nyilvánvalóan gyanús volt számukra az oktatók többségének beállítottsága, de egy prózaibb oka is volt a döntésnek: számos iskolaépületet szándékoztak börtönné és siralomházzá alakítani. Hamar felismerve az oktatási rendszer csődjét – például egyetlen nemzet sem nélkülözheti a hadiiskolákat – iskolareformról döntöttek. Az újjáépítési hullámban az École Polytechnique-t, „Műegyetemet”, mely a mai napig nagy presztízsű felsőfokú tanintézmény, csak 1797-ben alapították. Monge a létrehozásának minden fázisában döntő szerepet játszott, ő lett az első igazgatója is. A forradalom „késő konvencionális”, majd brumaire-i szakaszába az mentette át a jakobinus Monge-t, hogy még miniszterként megismerkedett és összebarátkozott Napóleonnal (1769–1821). Az itáliai és egyiptomi expedíciókban fontos diplomáciai feladatokat kapott, sőt – második szégyenfolt – tagja lett a Commission des Sciences et des Arts en Italie-nek, Az Itáliai Tudományok és Művészetek Bizottságának, melynek küldetése az volt, hogy az 1797-es campoformiói béke rendelkezésének megfelelően itáliai műkincseket vételezzen a Francia Köztársaság számára. 1798-ban Napóleon létrehozta a hasonlóan eufemisztikus nevű Institut d’Egypte-et (Egyiptomi Intézet), melynek fejévé Monge-t tette meg. Egyiptom 1801-es térdre kényszerítése után Napóleonnak számos mérnök segítségére kellett támaszkodnia a a speciális hadi igényekhez igazított helyi infrastruktúra kiépítéséhez. Az évek során ebben nagy szerephez jutottak az École Polytechnique-ben végzett hallgatók. Brumaire 18-adika után az első konzul kegyei sokaságával halmozta el Monge-t. Többek közt a Becsületrend főtisztje lett (ez tehát ennyit jelent…), élethosszig tartó szenátor, a szenátus elnökhelyettese, és, keserűen mondva, hajdani jakobinusként Pelusium grófja. (Ez utóbbi minden címe közül vitathatatlanul a legnevetségesebb.) 1806-ban engedelmesen, Napóleon akaratához igazodva a szenátus elnökévé választották. A Bourbon restauráció 1815-ben minden kitüntetésétől és posztjától megfosztotta. Monge-nak rejtőzködnie kellett, csak 1816-ban térhetett vissza Párizsba. (A történtek ilyetén lefolyása mindenesetre felvillantja a különbséget terror és terror között.) Monge-ot súlyosan megviselte lelkiekben, hogy senki sem állt ki mellette. Ez hozzájárulhatott egészsége leromlásához, mely két év alatt a sírba vitte. Bár elhagyatottként, megvetettként ment el, voltak, akik hálával gondoltak rá, és koszorút vittek a Père Lachaise-beli sírjára.

Monge életműve
Az 1794-es thermidori fordulat, a forradalmi terror véres felszámolása hajnalán, feltehetnénk, Monge az átmenekülése politikai részleteivel volt elfoglalva. De éppen akkoriban fejezte be legmaradandóbb művét, az Ábrázoló geometriát. Ez elgondolkodtató. Azt a gyanút erősíti, Monge politikai nézeteit, ha voltak egyáltalán, legyenek bár őszinték vagy sem, életműve elősegítéséhez igazította. Hiszen egyaránt megfelelt a francia történelem temps fortja, „nagy ideje” minden szakaszának, és ezt csak a „kis idők” beköszöntével olvasták a fejére, ami előtt értetlenül állt. Ha akadémiai és tudományos életére pillantunk, elsőre nem is értjük, hogy maradhatott ideje politikai aktivitásra – hacsak spekulatív úton arra a lapos bölcsességre nem jutunk, hogy a tudományos karrierhez az érdekében eltöltött sok idő, a politikaihoz viszont a kevés idő hasznos, mely nem engedi a belegabalyodást a politikacsinálás kínosabb technikai és becsületbeli részleteibe.
Monge tudományos munkásságát mindvégig meghatározza a közelség a legkézzelfoghatóbb valósághoz. Legnagyobb pillanataiban nem felfedez, hanem láttat, pontosabban felfedezi a láttatás újabb és újabb elveit. A matematika területén is nagyot alkotott, de ott sem az absztrakció, hanem a geometria területén. Közelebbről a differenciálgeometriáén, melynek akkori csúcseredményei néhány évtizedes múltra tekinthettek vissza Leonhard Euler (1707–1783) munkássága nyomán. A „francia iskola” olyan kiválóságot is felmutathatott, mint a már említett Clairaut, vagy Jean Baptiste Marie Charles Meusnier de la Place (1754–1793). A terep tehát mind szakmailag, mind „szakmapolitikailag” nehéz volt, Monge mégis érvényeset, maradandót, rá jellemzőt tudott alkotni. A differenciálgeometria terén műve két részre osztható. Az egyik az akkor már klasszikus területnek számító felületi görbék és felületek görbületi viszonyai, burkolói és a kifejthető felületek. Első nagyobb értekezései ezekről születtek a nyolcvanas években. A másik, modernebb területet nagyobb figyelemnel övezte az utókor. Ez pedig – csak a zenéjére figyeljünk, a hely szűke nem enged matematikai részletezést – az elsőrendű, nemlináris parciális differenciálegyenletek, a legkevesebb értelmes dimenzióban röviden az F(x, y, z, p, q) = 0 alakú egyenletek (alkalmasan sima F függvényekre), ahol p-vel és q-val a keresett z megoldásfelület x, illetve y szerinti parciális deriváltjait jelöljük. A karakterisztikus sávok módszere felfedezésének körülményeit sokáig homály fedte, mígnem bebizonyosodott, hogy az elsődlegesség egy „rejtélyes”, feltehetőleg fiatalon meghalt, egész életében semmit nem publikált matematikusé, Paul Charpit de Villecourté (†1784). A bizonyítás és maga az elv részletei finoman szólva odafigyelést igényelnek. Itt lép „képbe” Monge, aki ezt megkönnyíti az egyetemi hallgató számára, egyúttal a saját korábbi kutatásaira is támaszkodva összeköti azt a klasszikus differenciálgeometriával. Szemben a közönséges differenciálegyenletekkel, a parciálisok megoldásterének legáltalánosabb szerkezete is meglehetősen rafinált. Monge láttatása ennek megértéséhez is segítséget nyújt. Ötlete igen röviden összefoglalható. Az adott egyenlet a tér egy pontjában az azon a ponton áthaladó lehetséges megoldásfelületekre speciális feltételt ró: a parciális deriváltak közti összefüggés alapján egy kúp, az úgynevezett Monge-kúp fektethető fel – mely persze fajulhat síkká és lineáris esetben egyenessé –, melyet a megoldásfelület érint abban a pontban, így a megoldásfelület maga is egy kúpsereg burkolójaként fogható fel. Magától értetődik, hogy itt általános kúpra kell gondolnunk – azaz nem okvetlenül körkúpra, hanem olyan felületre, amely egyenes alkotókból tevődik össze, azaz „egygörbületű”, és ezek egy csúcsban találkoznak. Tanulmányainkban az illusztrációk körkúpokra szorítkoznak, de ebben maga Monge is „ludas”, mert ő maga is ezzel az egyszerűsített ábrázolással kívánta elméletének megértését megkönnyíteni. 1807-ben készített magyarázó ábrája ennél többet is mutat. A megoldásfelület úgy érintkezik a kúppal, hogy utóbbi egy alkotója érinti a felületet a csúcspontnál. Ezek a felületi irányok felületi görbéket határoznak meg, melyeknek sok nevet adtak már, például karakterisztikus vonal, fokális vagy egyszerűen Monge-görbe. Ez is előrajzolódik Monge ábráján:
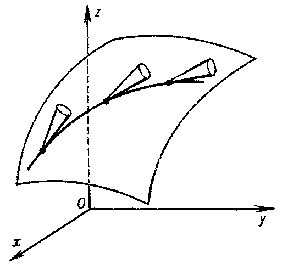
A POV-Ray rajzolóprogram korában nem kényszerülünk efféle egyszerűsítésekre, sőt, az is bemutatható, hogy a kúpsereg egy felület megjelenített képén túl is folytatódik. Az első rajzon egy megoldásfelület, két Monge-kúp és egy Monge-görbesereg látható, a másodikon az egyetlen Monge-görbét kúpsereg rajzolja ki. Itt – provokatívan – maga a megoldásfelület egyenes körkúp. (Mondani sem kell, hogy mindig kettős kúpokról beszélünk, melyek a felület két oldalán húzódnak.)

Monge kémiai munkássága ha nem is mélyenszántóbb a geometriaiénál, mindenesetre kalandosabb. Georg Ernst Stahl (1659–1734), I. Frigyes (1657–1713) porosz király háziorvosa vitán felül kiemelkedő vegyész volt, akinek legismertebb, tudománytörténeti szempontból legemlékezetesebb tette az volt, hogy a magáévá tette és formába öntötte Johann Joachim Becher (1635–1682) flogisztonelméletét. Az elmélet azt mondja ki, hogy égéskor nem gyarapodik az égetett anyag (oxigénnel), ellenkezőleg: eltávozik belőle egy egyre mesésebb tulajdonságokkal felruházott anyag, a flogiszton. Így például a fém a kalx és a flogiszton vegyülete, és égetésével a kalx, azaz a fém-oxid marad vissza az eltávozó flogiszton nyomán; a kalx flogisztont vehet át az azt bőven tartalmazó anyagokból, például a szénből, és így fémmé redukálható (mai szóval). Jean-Paul Marat-val (1743–1793) együtt – de ellentétben Marat nagy tudományos ellenlábasával, Antoine-Laurent Lavoisier-vel (1743–1794) – Monge is a flogisztonelmélet híveként indult, olyannyira, hogy társfordítója volt Richard Kirwan (1733–1812) ír geológus, a flogisztonelmélet egyik utolsó mohikánja 1787-es szakkönyvének. Monge azonban elsősorban volt tudós, másodsorban politikus, és miután meggyőzte őt Lavoisier (máig tartó, elfogadott) ellenelmélete, „átállt” a tudományos táborába. 1788-ban megismételte egyes jeles elődök kísérletét a „nehéz levegő”, azaz a szén-dioxid dekompozíciójára elektromos szikrákkal. Joseph Black (1728–1799) volt az, aki 1755-ben felismerte a magnézium elemi mivoltát, és 1754-ben megtalálta a magnesia alba, „fehér magnesia”, vegyi összetétele szerint magnézium-karbonát hőbontásával előállt gázt, melyet ma szén-dioxidnak mondunk, és ő (lúgok által leköthető) fixed airnek, azaz régi magyar kifejezéssel „nehéz levegőnek”. Bár Monge szóhasználatában – az oxigént „deflogisztált levegőnek” nevezi – még a flogisztonelméletet követi, következtetéseivel nyílt színi csapást mér az elmélet híveire. Jean-François Clouet-val (1751–1801) 1801-ben cseppfolyósították a kén-dioxidot, ami tudománytörténeti kuriózum, mert ez az első feljegyzett esete tiszta gáz (azaz nem elegy) cseppfolyósításának. Ők maguk azonban ezt nem tartották publikálásra érdemesnek. 1789-ben Monge meggyőző kísérleteken keresztül behatóan tanulmányozta a hajszálcsövességet. Eredményei felkeltették Pierre-Simon de Laplace (1749–1827) figyelmét, aki 1805-ben megvizsgálta a matematikai leírás lehetőségét. Monge, korának mintegy szokása szerint, a színek elméletével is foglalkozott, de itt igazi nagysága a maga tudása (és általában az akkori tudás) határainak megállapításában mutatkozott meg, továbbá feljegyzéseiben a kor tudósainak a tárgyban tett megfigyeléseiről. A délibábok optikájának magyarázatában ügyesen támaszkodott a fényvisszaverődés és fénytörés akkor már ismert elméletére. Nem kerülhette el a figyelmét az izlandi pát kettős fénytörése sem, de 1786-ban nem érezte meggyőzőnek saját elképzeléseit a jelenség magyarázatáról. Bíráló megjegyzései a tárgyban tett egyéb elméletekről azonban értékes optikatörténeti hozzájárulások. Balszerencsés módon 1790-ben a meteorológiába is belekapott, és noha kísérletei alaposságához nem fér kétség, a levegő vízgőztároló kapacitására alapuló magyarázatai részben leegyszerűsítők, részben korszerűtlenek voltak. Kivívta velük egy vérbeli svájci meteorológus, Jean-André de Luc (1727–1817) haragját. A svájci tudós ugyanott, az Annales de Chimieben (Vegytani Feljegyzések) egy ellencikkben attól óvott, hogy egy ember, aki sem a meteorológiához, sem a társterületeihez nem ért, vissza ne vesse harminc évvel a megértést.

Sok formai hasonlóság körvonalazódik a flogiszton- és a caloricumelmélet között. A caloricum vagy hőfolyadék az a feltételezett anyag, amely különféle áramlásaival maga okozza a hőtani jelenségeket. Ha visszaidézzük elemi kalorikus tanulmányainkat, azt találjuk, hogy egy efféle anyag feltételezése valóban elég sokáig ellentmondásmentesen elvisz bennünket a hőtani folyamatok magyarázatában, ám fennakad a hő- és mechanikai energia átjárhatóságának jelenségénél, amelynek részletes vizsgálata aztán meg is szüntette magát a tant. Kidolgozója Joseph Black volt. Érdekes módon a flogisztonelmélet ősellensége, Lavoisier a caloricumelmélet odaadó hívéne bizonyult. Monge az 1782 és 1832 között kiadott monumentális Encyclopédie Méthodique, Szisztematikus Enciklopédia CALORIQUE címszavában kimerítően bemutatja a kor felfogását a hőfolyadékról, de erre ma már csak mint tudománytörténeti érdekességre tekint az olvasó.
1790-ben a Nemzetgyűlés pontot akart tenni annak a próbálkozássorozatnak a végére, amely egységesíteni kívánta a kaotikus francia mértékrendszereket, és a decimális rendszer kidolgozásával bízta meg az Akadémiát. A hosszmérték, a méter bevezetésének mikéntjéről írt vastag jelentést készítő csapatban jóformán mindenki ott volt, aki „számít”, többek között Monge, Meusnier, Borda és Joseph-Louis Lagrange (1736–1813) gróf. Az inga lengésidejét alapul vevő elvet annak önkényes pontjai miatt elvetették, és magát a Földet vették mércéül: természetesen nem egy teljes hosszúsági kört vagy az egyenlítőt, hanem annak pontosan ismert arányú ívét (Dunquerque és Barcelona között). 1793-ra készült el a nagy mű.
***
Monge pályája tükörképe egy olyan kornak, melyet jobb szó híján „nagynak”, „óriásnak” mondtak (olykor talán tartottak is) hajdanán, amíg a történelemtudomány fel nem tárta ennek a kornak számos „kicsinységét”. Az alacsony sorból magát felküzdő zseni a bukás pillanatában nem értette, mi lehetett népszerűsége elvesztésének oka. Ha lehet mondani, ez az értetlenség az, amelyik tisztázza őt. Mégpedig a legrosszabb vád alól, amely annak a korszaknak illusztris figuráit méltán illeti: hogy cinikus kurzuslovag lett volna. Életműve java halhatatlan, és a többi része sem mondható érdektelennek.
Ezt olvastad?
További cikkek
Prostitúció a 19. századi Budapesten – Völgyi Réka az elBeszélő vendége
Völgyi Réka írja a Budapesti Levéltári Mozaikokban: „Milyen volt az élet a századfordulón egy budapesti bordélyban? Sajnos a levéltári iratanyagokban nem maradt fenn olyan forrás, amin keresztül egy konkrét bordélyház […]
Kresz Mária – a gyermekélettől a népviseleteken át a népi kerámiákig
„Tanulmányozta a cserepek motívumait, szimbólumait, és összehasonlította azokat a régi, különösen az ázsiai kultúrákban fellelhető emlékekkel. A kerámiák motívumait összevetette a szőttesek, hímzések és fafaragások díszítésével is. Minden kutatásánál a […]
Bartucz Lajos – egy meghatározó antropológus életútja
Bartucz Lajos foglalkozott rassztörténettel, a gyermekek testi fejlődését, illetve a katonák termetét vizsgálta. Rengeteg leletanyag összegyűjtését köszönhetjük neki, amelyeken keresztül a magyarság antropológiai összetételét kutatta és publikálta. Megjelent négy könyve, […]
Előző cikk
„A doktori képzést ne mindig problémaorientáltan közelítsük meg” – Kerekasztal a fiatal kutatók helyzetéről és lehetőségeiről
A fiatal kutatók helyzete és lehetőségei című kerekasztal-beszélgetést a Szegedi Történészhallgatók Egyesülete (SZETE) harmadik, 2021. április 8–9-én megtartott konferenciájának kísérőprogramjaként rendezték meg. Az érdeklődők a SZETE Facebook-oldalán követhették az eseményt, […]













