Az integrálszámítást megalapozó(?) polihisztor – Gottfried Wilhelm Leibniz élete
Leibniz szellemi csúcsteljesítményéhez ma már nem fér kétség. A plágiumvádak alól, amelyeket Newton egy svájci hódolója, majd munkatársai ültettek el Newtonban, az utókor teljes egészében felmentette. Különös békediplomáciájában nem könyvelhet el közvetlen sikereket, de leírt gondolatai nem mentek veszendőbe. Provokatív filozófiai téziseit számos gúny érte (a csodálat mellett), de Leibniz nyugodtan pihenhet: álláspontjai megkérdőjelezhetők, de a cáfolatokkal még adós a mindmáig erős ellentábor. Kényszerű szerkesztési szükség kettéválasztani „írói munkásságát” és mindazt, amit a tudomány terén létrehozott, de ezek néhol nem is rejtett összefüggéseit nem hagyom figyelmen kívül a továbbiakban, arra is súlyt helyezve, hogy a vesztfáliai béke (1648) után kialakult történelmi helyzetet, annak döntő hatását Leibniz életművére szintén felvázoljam. Anekdoták rovására is, melyek különben is megbízhatatlanok.
Leibniz élete
Lássunk előbb egy rövid és célratörő családtörténetet. Wilhelm Schmuck (1575–1634) lipcsei jogászprofesszor lánya volt Catharina Schmuck (1621–1664). Ambrosius Leibnütz (1569–1617) városi jegyző anyai ágon nemesi származású fia az erkölcsfilozófia lipcsei professzora és tanszékvezető-helyettese, Friedrich Leibniz (1597–1652). Catharina Schmuck és Friedrich Leibniz gyermekeként született Gottfried Wilhelm Leibniz (1646–1716) Lipcsében, július elsején éppen 375 éve. Azaz mind szellemileg, mind anyagilag jól szituált házba. A messze múltban – a családnév Braunschweigben a XV. században bukkan fel először – az ősök az apai ágon, a vezetéknév korabeli jelentése alapján, pékek lehettek.

Hogy csodásak-e a jelek, melyek legapróbb korától kísérték növekedtét, mint az, hogy kétévesen leesve az asztalról sértetlen maradt, joggal fogadja szkepszissel a laicizálódott utókor, de a tény, hogy a családja ezekre mint jelekre tekintett, nyilvánvalóan kihatott lelki fejlődésére. A gyermek hatéves korában veszítette el édesapját, így erkölcsi nevelésének jó részét édesanyjának köszönheti. Örökségként rá maradt apja könyvtára, amelyet hétéves korától kezdve látogathatott. Első iskolája a Nikolaischule volt (Szent Miklós Iskola, neve a templom közelségéről). Ez Lipcse legrégebbi polgári iskolája, 1512 és 1872 között működött. Wagner (1813–1883) ugyanennek az intézménynek volt „vásott kölyke”, ellentétben a kis Leibnizcel, akiről semmi effélét nem jegyeztek fel, de ez nem is valószínű, ha egyszer tanulmányai mellett tizenkét éves korára csinosan megtanult latinul. (Ennek fokát ugyan nem ellenőrizhetjük.) Ekkor kezdett a görögbe. 1659 pünkösdjén rukkolt elő maga költötte háromszáz hexameteres versével. 1661-től, 15 éves korától volt diákja a Lipcsei Egyetemnek. Ez a heidelbergi mellett a legrégebbi és legpatinásabb felsőfokú tanintézménye volt a német birodalomnak. Megalapítását IV. (Luxemburgi) Vencel (1361–1419) cseh királynak köszönheti, aki a huszita mozgolódásokkal összefüggésben elmozdította a Prágai Egyetem rektorát, Johannes Otto von Münsterberg (1360?–1416) teológust, ő pedig a német hallgatóival kivonulva 1409-ben studium generalét hozott létre Lipcsében, melynek alapításához, őrgrófi támogatással, az évben V. Sándor (1339–1410) pápa adta aláírását. Az egyetem jeles hallgatói közé tartozott Gellert (1715–1769), akinek 1757-ben publikált vallásos verseire Beethoven (1770–1827) írt hat dalt (op.48) 1801 és 1802 között.
A klasszikus auktorokkal kezdve Leibniz a humaniórákban igen korán elérkezett a skolasztikus filozófiáig. Bár vannak, akik e tanulmányaira mint kidobott időre tekintenek, saját maga szavai azt tanúsítják, ez nincs így. Nem volt ugyan túláradó a tisztelete az egyházatyák írásművészete iránt, de azon a véleményen volt, hogy segítették őt annak felismerésében, mi az a legvégső kifinomultság, ameddig az emberi elme egyáltalán eljuthat. Mindenesetre ismereteivel már tizenhét évesen meghökkentette tanárait. Tizenöt éves korára tartott a „moderneknél”, mint például René Descartes (1596–1650). Leibniz tehát bámulatos szívóssággal építette fel saját ismereteit a régi és új filozófiából, mielőtt nemhogy a maga rendszerét kidolgozta, de saját nézeteivel előhozakodott volna. Egyetemi (jogi, filozófiai) tanulmányai befejeztével, 1663-ban a bakkalaureátust (kb. „egyetemi doktori fokozat”) elnyerte ugyan Lipcsében, de a jogtudományi doktori címtől visszatartotta őt túlságosan fiatal életkora. Az egyetem talán elmagyarázta az ifjú titánnak, akiről honnan is sejthette volna, hogy hamarosan ő lesz „a” Leibniz, hogy ridegségük nem a pályaműnek szól: mindössze nem akarják elvonni a tudósközösség jogát a megítélésre, melyre nem kínálkozott alkalom, lévén a jelölt tizenhat éves. Akárhogy is, a máskülönben nyugodtnak mutatkozó Leibniz dühbe gurult. Átvonult az Altdorfi Egyetemre, ahol 1667-ben el is nyerte a doktori címet.
Az egyetem, korábbi közel fél évszázados akadémiai státusából – ebben az intézményben nevelkedett Szenczi Molnár Albert (1574–1634) is –, II. Ferdinánd (1578–1637) császártól nyerte el rangját 1622-ben. 1809-ben, miután mind Erlangen, mind Nürnberg (és az ahhoz közeli Altdorf) Bajorországhoz került, a régi rivalizálást a háborús elszegényedésre hivatkozva I. Miksa József (1756–1825) bajor király Erlangen javára oldotta fel az Altdorfi Egyetem felszámolásával és vagyonának az Erlangeni Egyetemre ruházásával.
A doktori cím odaítélésével párhuzamosan a különösen megelégedett egyetem professzori címet is felkínált az akkor még szinte kamasz Leibniznek, aki azonban azt visszautasította. Igazságtalannak érzem Sarah Tietz álláspontját. A Svájcban kutató filozófus ezt Leibniz illúzióvesztésével magyarázza a német akadémiai rendszer merevsége láttán. Hiszen Leibniz személyében éppen annak nyájasságát, befogadó hajlamát tapasztalhatta. Ugyanakkor az előtte feltáruló alternatív életpálya vonzónak tűnhetett a számára.
János Keresztély, Boyneburg szabadura (1622–1672) jénai és helmstedti egyetemi évei, majd udvari szolgálat után felkérést kapott János Fülöp (1605–1673) érsek-választófejedelemtől, hogy fogadja el a mainzi udvarmesteri, majd államkancellári posztját. Ennek feltétele az volt, hogy Boyneburg áttérjen a katolikus hitre. Erről közvetlenül a kor harcos apologétája, a jezsuita Jodocus Kedd (1597–1657) győzte meg. A döntés nem esett nehezére, hiszen eleve a két felekezet közti béke hívének számított, ami öt évvel az 1648-as vesztfáliai béke után sokak természetes törekvése volt. Helmstedt volt az egyik központja az irénizmusnak (az εἰρήνη, eirene görög „béke” szóból), mely a felekezetbékét szorgalmazta, és amely irányzatnak Boyneburg mellett másik kulcsfigurája az Európa-szerte, így Magyarországon is vallásegyesítést sürgető Cristóbal de Gentil de Rojas y Spinola (1626–1695) bécsújhelyi püspök. Természetesen nézőpont kérdése, az irénizmus mennyiben tekinthető a felekezet érdekeit feladó vagy veszélyeztető, netán áruló felfogásnak. Boyneburg viszonya is megromlott a jezsuitákkal, akik elérték, hogy a választó 1664-ben megvonja tőle bizalmát, sőt, rövid időre le is tartóztatták.
Bár a napi politikai életet ezt követően nem alakíthatta, befolyása megmaradt. Egy különösen jól sikerült nürnbergi vacsora meggyőzte őt arról, hogy Leibniz nemcsak rendkívüli szellemi képességekkel van megáldva, de konciliáns természete mintha az ő világnézetének lenne folytatása. 1667-ben azt tanácsolta neki, ajánlja János Fülöpnek egy jogi reformmal foglalkozó traktátusát. A választó ezt tetszéssel fogadta, és szolgálatába invitálta Leibnizet. Azonnal megbízták a mainzi corpus juris átfogalmazásával. Leibniz élénk levelezést folytatott Jacques-Bénigne Bossuet (1627–1704) katolikus püspökkel. Irénikus törekvéseinek legalábbis szellemi tetőpontja a Systema Theologicum, A teológia rendszere, amely a hittudományt katolikus alapon építi fel. Hogy a politikailag csavaros észjárású, de hitbéli kérdésekben képlékenyen alakítható választó mennyiben tekinthető maga is irénikusnak, kérdéses, de éles szemmel ismerte fel, hogy a Párizsban nevet szerző Leibniz alkalmassá tette magát egy kényes diplomáciai küldetésre. XIV. Lajos (1638–1715) területi ambíciói aggodalommal töltötték el a német fejedelemségeket. A mainzi választó úgy gondolta, Leibnizre oda fognak figyelni, ha előadja fantasztikus Consilium Aegyptiacum, Egyiptomi terv című elképzelését, melyben a Napkirályt egyiptomi hadjáratra ösztönzi. 1672-ben utazott a tudományos világ akkori központjába, és bár küldetése sikertelen volt, személyes életére az út döntő hatást gyakorolt. Az élő „modernek” közül Christiaan Huygens (1629–1695) befolyása volt a legdöntőbb. Párizsba látogatásának kezdetén Leibniz nem vonzódott a matematikához. A kor matematikájában nem mozgott otthonosan, sir Isaac Newtonnal (1643–1727) akkor még kölcsönösen nem tudtak egymásról. A már elmentek közül, több publikálatlan írásuk megismerése révén, Descartes és Blaise Pascal (1623–1662) hatása volt a legnagyobb az ifjúra. Leibniz maga állította később, hogy az analízis: differenciál- és integrálszámítás, a végtelen sorok elmélete Pascal olvastán fogamzott meg benne. 1673-ban egy londoni útnak is szerét ejthette. Miután világossá vált, hogy XIV. Lajos nem hajlik Egyiptom megtámadására, János Fülöp hasonlóan Európa-pacifikáló diplomáciai küldetéssel küldte az angol fővárosba saját unokaöccsével, Menyhért Frigyessel (1644–1717), Schönborn és Buchheim birodalmi szabadurával együtt. Megbízatásuk, melyet nem tudtak végbevinni, egy francia–angol–holland béketárgyalás keresztülvitele a német részvétellel. Londonban egyik első útja honfitársához, Henry Oldenburg (1619?–1677) teológushoz, a Királyi Társaság titkárához vezetett. Előttük mutatta be a négy alapművelet elvégzésére alkalmas számológépét. Már ott eltökélte, hogy a fából készült, fogaskerekes szerkezetet rézből készítettre fogja cserélni, amit újra és újra továbbfejlesztett, ami 1690-ben vezetett a machina arithmeticához, az „aritmetikai géphez”. (Tizennégy kilós mintadarabja feledésbe merült, míg 1894-ben meg nem találták a Göttingeni Egyetem padlásterében. A korábbiaknak nyomuk veszett.) Az ötlet nem Leibnizé volt. Az első mechanikus számológépet, mely, jóllehet, primitívebb az övénél, Wilhelm Schickard (1592–1635) szerkesztette. Leibniz ötleteit a későbbi mechanikus számítógépekben évszázadokig alkalmazták, és bár az övé nem működött, Londonban mégis akkora tisztelettel fogadták, hogy ifjú kora ellenére befogadták a Királyi Társaságba. (Ekkor még mindig csak huszonhat éves volt!)

A választó halála miatt, diplomáciai küldetése félbeszakadván, Leibniz visszautazott Párizsba. Ott nem járt akkora sikerrel: a Párizsi Akadémia a tagságot ahhoz kötötte volna, hogy áttér a katolikus hitre, amit ő visszautasított. (Mindamellett jóval később, 1700-ban külső tagnak választották.)
1676-ban tért vissza német földre, nagy, londoni-amszterdami-hágai kitérővel. Ennek az útjának során találkozott szemléletének nagy alakítóival, a mikroszkóp kifejlesztőivel, Jan Swammerdammal (1637–1680) és Antonie Philips van Leeuwenhoekkel (1632–1723). Behatóan kezdett érdeklődni az orvostudomány iránt. Pietikus álláspontja alapján, amellyel azt fejtegeti, az orvoslás a legfontosabb valamennyi természettudomány közül, mert nemcsak fenntartani, de fejleszteni is igyekszik az emberi testet, és ilyenformán eszköze annak, hogy az ember Isten dicsőségére munkálkodjék, azt hihetnénk, érdeklődése teoretikus szinten maradt. Melléfognánk: a korszellemtől eltérően a kevesek közé tartozott, akik a kísérletekre, megfigyelésekre súlyt helyeztek.
János Frigyes (1625–1679) braunschweigi herceg, Calenberg-Göttingen fejedelme már a választófejedelem halálát követően, 1673-ban könyvtárosi és tanácsosi állást kínált Leibniznek Hannoverben, aki azonban párizsi alkalmaztatás reményében eleinte vonakodott, majd végül két évre rá kötélnek állt. 1676-ban foglalta el állomáshelyét, és bár rengeteget utazott, élete végéig Hannoverben élt. Feladatai változatosak voltak, például megszervezte a Harz hegység ezüstbányáinak víztelenítését. Ehhez, paradox módon vizet szoktak használni: vízerőgépek segítettek a lenti folyadék kiszivattyúzásában. Ott azonban efféle vízenergia nem állt rendelkezésre, ezért Leibniz „malmokat”, azaz szélerőgépeket használt céljához. Az eljárást úgy tökéletesítette, hogy az energiakinyerést függetlenítette a széliránytól. 1685-ben azonban a bányaigazgatóság az első hibánál felfüggesztette a gépek működését. Nyomasztotta őket, hogy nem értik a mechanizmust.
A herceg halálát követően Leibniz kiesett a kegyből, mert sem választófejedelmi utódai: a herceg öccse, Ernő Ágost (1629–1698), majd annak fia, György Lajos (1660–1727), a későbbi I. György brit király nem táplált rokonszenvet iránta. Szorult helyzetéből a nagy hannoveri nőalakok: Ernő Ágost felesége, Zsófia (1630–1714) pfalzi hercegnő, majd lánya, Hannoveri Zsófia Sarolta királyné patronátusa és inspiratív barátsága segítette ki. Leibniz hannoveri munkálatai természetesen nem szorítkoztak bányamérnökösködésre. A francia fél által, területi és kereskedelmi engedményekért Hollandia ellen indított, de számos más hatalmat is érintő háborút lezáró nijmegeni békéhez kapcsolódó 1679-es bilaterális szerződésekhez, melyekhez a német birodalom is csatlakozott, Leibniznek ki kellett dolgoznia a szuverenitás új teoretikus koncepcióját. Ernő Ágost megbízta őt a Braunschweig-ház történetének megírásával is, jó okkal: jogi igényeinek megalapozására kívánta azt felhasználni. Leibniz azonban másképp fogta fel a feladatot. Tökéleteset akart alkotni, számára mellékes aktuálpolitikai körülményektől mentesen. Keresztül-kasul beutazta a térséget, még Itália földjére is ellátogatott dokumentumokért, melyek hatalmas volumene végül „agyonnyomta” magát a művet: soha nem készült el, bár befejezett előszavát nagyra tartják. Élete végét egy sötét disputa árnyékolta be. Ennek átlátásához meg kell ismerkedjünk tudományos életművével.
Leibniz matematikája és fizikája
Párizsba érvén Leibniz matematikai felkészültsége, beleértve mind előképzettségét, mind matematikusi hajlamait, alacsony szinten állt. Ennek okát abban találhatjuk meg, hogy nem volt tájékozott a „modernek” munkájában. A kor jeles matematikusához, Ehrenfried Walther von Tschirnhaus (1651–1708) grófhoz 1680-ban írt levelében tréfásan emlékezik meg arról az esetről, amikor az Arkhimedes (Kr.e. 287?-212) által feltárt és bevezetett súlypontról tévtant hirdetett (mely érdekes módon a mai napig tartja magát egyes fejekben). Egyes „hétköznapi” síkbeli alakzatok példájából arra az indokolatlan következtetésre jutott, hogy a súlyponton átvezetett egyenes szükségképpen felezi az alakzat területét. A vele rokonszenvező Huyghens, amikor előadta neki „felfedezését”, kacagásra fakadt, amit Leibniz nem vett rossz néven (nem volt kolerikus alkat), ellenkezőleg, ösztönzésnek tekintette, hogy nekilásson Eukleides (Kr.e. 300?-?) Elemei tanulmányozásának. Sok időt eltöltött a Pascal-háromszög tanulmányozásával, mert nem tudta, hogy amióta a híres számelrendezés feltűnt Peter Bennewitz, ismertebb „tudományos nevén” Petrus Apianus (1495–1552) 1527-ben kiadott Aritmetikája címlapján, annak felépítését széltében-hosszában tanulmányozták, mígnem Pascal 1665-ös értekezése betetőzte a vizsgálatokat. Ugyanakkor jelentős eredményeket tudott felmutatni egy klasszikus területen, és ez mintegy „előszobája” volt az integrálszámítás felfedezésének és kezdeti formájába öntésének. Sokrates (Kr.e. 469–399) vitapartnere, a kiemelkedő ügyvéd és matematikus, Szofista Antifon egy ismeretlen területű alakzatot egyre jobban „kimerített” átfedéstől mentes ismert területűekkel, és ilyenképpen egyre jobb közelítését kapta az ismeretlen területnek – a kilikiai Simplikios (490?–560?) legalábbis neki tulajdonítja az ötletet. 1647-ben Grégoire de Saint-Vincent (1584–1667) az eljárást methodus exhaustionibusnak, „a kimerítés módszerének” nevezte. Az ötlet szövevényes fejlődéstörténetét mintegy megkoronázta Bonaventura Cavalieri (1598–1647) 1635-ben publikált, a gyakorlatban is könnyen alkalmazható elve az „oszthatatlanokról”, melyet „transzmutációnak” neveztek el. Amit Leibniz ehhez hozzátett, azt a mai szóhasználatban a parciális és a helyettesítéses integrálás fogalmaival írhatnánk le. A kor egy másik nagy érdeklődést kiváltó területe, a (végtelen) soroknak inkább gyakorlata, mint elmélete szintén megragadta Leibniz figyelmét. Noha a konvergenciafogalom akkoriban még nem fogant meg a legnagyobbak fejében sem, egyes eredményei a mai elvi precizitás próbáját is kiállják. A mai szóval sorfejtéssel előállított híres eredménye láttán már Huyghens sem kacagott.
A sor iskolapéldája a Leibniz-típusú soroknak. Azok a tanítók kedvelik különösen ezt a típust, akik élvezetet lelnek különösen lassan konvergáló végtelen összegek felmutatásában – éppen emiatt az adott formula is meglehetősen alkalmatlan a π közelítő értékének meghatározására. (Amint azt ki-ki egy közönséges Excel-programmal pillanatokon belül ellenőrizheti, az első tízezer tag összeadásával körülbelül 3,14149265359-ot kapunk, míg a π meglepően hasonlóan, de mérnöki szemszögből súlyosan eltérően indul: 3,14159265359…) De ez nem számít egy teoretikus eredmény esetén, mi több, valamelyest még örvendetes is, mert efféle képletek megalkotói és megbecsülői kezdik áttenni a súlypontot az „arkhimedesi” (mérnöki) matematikáról az „eukleidesire” (az elméletire). Kora válogatja, melyik ágat kell erősíteni.
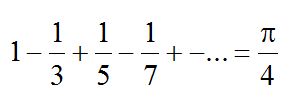
A kettes számrendszer alkalmazásának gyökerei egészen az ősi Egyiptomig nyúlnak vissza. Európában elsőként Thomas Harriot (1560?–1621) alkalmazta (korában visszhangtalanul). Összeadásra, kivonásra, szorzásra is példákat találni a kézirataiban. Leibniz azonban nagyobb hírverést csinált a maga ettől független felfedezésének. 1679 táján támadtak az első gondolatai, de csak 1703-ban hozta nyilvánosságra elképzelését. Eredményére büszke volt, úgy tartotta, az 1 elegendő ahhoz, hogy mindent levezessünk a semmiből. Pierre-Simon de Laplace (1749–1827) szerint Leibniz a teremtés művét pillantotta meg a kettes számrendszerben, olyannyira, hogy azt Philippus Maria Grimaldi (1639–1712) jezsuita misszionárius közvetítésével a tudományokban jártas Kang-hszi (1654–1722) kínai császár megtérítésére is megpróbálta felhasználni.
Leibniz tudományszervező munkássága is kimagasló volt. 1682-ben Otto Mencke (1644–1707) filozófussal megalapítják a latin nyelvű Acta Eruditoriumot (A Műveltség Lapja), a német nyelvterület első tudományos újságját. Leibniz német akadémiák megalapítását szorgalmazta, így a Német Tudományos Akadémia (1700-as) megalapításának fontosságáról meggyőzte Zsófia Sarolta (1668–1705) porosz királynét.
Leibniz olyan pontokon is meghatározó figurája életünknek, amelyeken nem is gondolnánk. Robert Recorde (1512?–1558) walesi orvos és matematikus azzal tette magát híressé, hogy 1557-ben bevezette a ma is használatos egyenlőségjelet. Sajátos módon ezt a jelet többen, így François Viète (1540–1603) a kivonásra használták. Descartes levelezésében 1640-ben a mai értelemben és alakban fordul elő, de ő nyilvánosan (megfejthetetlen okból) a
![]()
jelet alkalmazta. Newton és Leibniz munkássága kellett hozzá, hogy Recorde egyenlőségjele Britannián túl terjedjen. (Descartes ugyanakkor „legyőzte” Recorde merev és ügyetlen jelölését a hatványkitevőkre, és bevezette a ma is használatos módot.) Azt lehet mondani, ebben Leibniz hozzájárulása csekély. Nem úgy az általa teljesen önállóan bevezetett : osztásjelben. (Angolszász országokban ezt ma kizárólag arányosságok felírásához használják.) Ugyancsak ő vezette be az integráljelet ( ∫ ) és a differenciálás jeleként a d-t.
A békeszerző, irénikus Leibniz élete „értelme” volt a kapcsolatépítés. Nem merész a feltételezés, hogy ennek lehetőségeit könnyebben megtalálta fejedelmi udvarokban, mint egyetemeken, céhérdekek hálójában. Mégis életének, sőt, az egész XVII. századi tudománytörténetnek a legszerencsétlenebb békétlenségéhez vezetett ígéretes londoni kapcsolatépítése. Első londoni útja alkalmával bizonyára nem találkozott személyesen is a matematika angol valódi „nagyjaival”, mert azok nem a fővárosban éltek, és nem tesz efféléről említést leveleiben. A jelentős fizikus-kémikus, a Királyi Társaság későbbi elnöke, Robert Boyle (1627–1690) 1667-ben írt The Martyrdom of Theodora and of Didymus, Thedora és Didymus vértanúsága című regényén alapul Händel (1685–1759) egyik utolsó oratóriumának, az 1749-ben komponált Theodorának (HWV68) a szövegkönyve.
Boyle házában – megbízója, János Fülöp választófejedelem halálának napján – találkozott az akkor mindenesetre nagy matematikusnak tekintett John Pell-lel (1611–1685). Mikor beszámolt neki egy algebrai fogásáról, Pell némileg megütközve hívta fel a figyelmét rá, hogy ez megtalálható François Regnauld lyoni matematikus egy Gabriel Mouton (1618–1694) abbé által kiadott csillagászati munkájában. Leibniz a hozzá közel lakó Oldenburg példányából szomorúan győződött meg Pell igazáról. Oldenburg azt tanácsolta, exkuzálja magát egy feljegyzésben, mivel a mű Párizsban hozzáférhető volt, és így Leibnizre a plagizálás árnya vetült. Leibniz így tett, leírta a maga gondolatmenetét is, és ez Oldenburgnak elég is lehetett. Pell azonban meg volt győződve a plagizálásról. Boyle maga is gyanakodhatott: nem léptek levelezésbe Leibnizcel.
Második londoni útja alkalmával John Collins (1625–1683) matematikus – bár ne tette volna! – átadta Leibniznek néhány matematikus, köztük Newton ki nem adott kéziratait. Ez lett az alapja a vádaskodásnak. Newton 1693-ban saját költségén Cambridge-be invitálta Nicolas Fatio de Duillier (1664–1753) bázeli matematikust és természetfilozófust. Fatio Newton hódolója volt, akinek szent meggyőződése szerint Leibniz a differenciál- és integrálszámítás gondolatát Newtontól lopta. Magában Newtonban efféle ötlet korábban nem merült fel, legalábbis Leibnizről írt leveleiben ez nem jelentkezik. Fatio többször megírta Huyghensnek is a feltételezését, majd 1699-ben nyilvánosság elé is állt a váddal. Az ügyben számos tudósi levél keletkezett. Newton 1703 és 1727 között volt a Királyi Társaság elnöke, ilyenként, mondhatni, kényelmes pozíciója volt a kényelmetlen ügyben. 1712-ben megjelent egy anonim válogatás Commercium Epistolicum, Levélgyűjtemény címmel ebből a levelezésből, melyről feltárták, hogy a válogató maga Newton volt. A játék kezdett elfajulni. Leibniz a szerző megjelenése nélkül nyilvánosságra hozta Johann Bernoulli (1667–1748) egy 1713-as levelét, melyben Newton hibájául rója fel a magasabb rendű differenciálok téves interpretációját. (A szerződés gyanúja ráterelődött Johann Bernoullira, aki azonban nyilvánosan letagadta azt, és ezt Newton is elfogadta.) Ez a húzás azonban nem lehet válasz Newton gyűjteményére, ugyanis azzal Leibniz csak a következő évben ismerkedett meg. Az adott elsőbbségi ügyben ugyan Newton hívei nem tudták kimutatni Leibniz rosszhiszeműségét, de Leibniztől nem állt távol dokumentumok, dátumok tudatos meghamisítása. A Commercium Epistolicum tartalmazza (a függetlennek éppen nem mondható) Királyi Társaság megállapítását Newton elsőbbségéről. Körülmények meglepő szövevénye vezetett oda, hogy az angol korona Anna (1665–1714) királynőről György Lajos hannoveri választófejedelemre szálljon. A Leibnizcel amúgy sem rokonszenvező uralkodó ejtette a tudóst, megtiltotta, hogy Anglia földjére tegye a lábát. A kegyvesztett, elhagyatott Leibniz 1716-ban halt meg Hannoverben.
Bár a vitában nemtelen eszközökhöz nyúlt, a vád igazságtalan volt. Newton az infinitezimális számításokhoz ugyan jóval korábban hozzálátott, mint Leibniz, de Leibniz fentebb már megismert párizsi munkássága bizonyítja, hogy a differenciál- és integrálszámítással, azok inverz kapcsolatával Newtontól függetlenül is tisztában volt. Legnagyobb eredményüket (az analízis alaptételét) ezért méltán nevezi az utókor Newton-Leibniz-szabálynak.
Fogalmaik mai igényű tisztázásával mindketten adósak maradtak, de ez mégsem írható a kor rovására. A matematikával is foglalkozó szolipszista ír püspök, George Berkeley (1684–1753) briliánsan mutatott rá a „végtelen kicsiny” fogalmi megalapozatlanságára. Éles bírálata sokat segített a matematikai analízis ma megkövetelt tisztaságának eléréséhez.
Kisebb hullámokat vetett, mégis messzebbre mutat egy másik vitás pont Newton és Leibniz között. Ori Belkind azonban szabatosan rámutat, hogy külső jegyek alapján a kettejük álláspontja közti különbségből nem szabad túlzó következtetéseket levonni. Miről is van szó? Newton hitt az abszolút, testektől függetlenül létező térben, míg Leibniz, aki a kiterjedést az anyagi testek attribútumának tekintette, ezt visszautasította. Kétségtelen, hogy a relativitáselmélet fényében Newton „fizikai” térelmélete tarthatatlan, csak éppen az nem igaz, hogy Newton ezzel a mozgások relativitásának elvét is visszautasította volna, vagy az, hogy Leibniz a maga „metafizikai” álláspontjával a relativitáselmélet előfutárának lenne tekinthető. Leibniz a fizika számos területével foglalkozott, így az optikával és a dinamikával is. Utóbbiban határozottan elutasította Descartes elveit. Leglátványosabb különbségük az, hogy Descartes a lendület, Leibniz a vis viva, élőerő (azaz a mozgási energia kétszerese) megmaradását hirdette. Természetesen ha precízen tisztázták volna körülményeiket, mindketten rájöttek volna, hogy mindkét mennyiség megmarad bizonyos feltételek mellett.
Mai finnyásabb korunkban hajlamosak vagyunk az intrikáknál, hamisításoknál is nagyobb bűnnek tekinteni, ha valaki érett fővel alkímiára adja a fejét, azon belül is a legszörnyűbbre: aranycsinálásra. Mint Leibniz (bővebben erről itt). De mérjünk egyenlő mércével: mint Newton. Mint Boyle.
Néhány szó Leibniz filozófiájáról
Kevéssé valószínű, hogy Leibniz eszmerendszeréről kialakított képünket fenekestül felforgatná, ha nyilvánosságra kerülne hatalmas hagyatékának mindmáig feldolgozatlan mintegy fele része. A rendelkezésre álló filozófiai írások is annyira szerteágazók, hogy még „könyvtári” számbavételük is komoly nehézségbe ütközik. Bár élete vége felé árnyat vetett rá a meglehetősen igazságtalanul rá vetülő plágiumvád, szellemi képességeit, filozófiáját, melyben a jeles „kibékítő” a klasszikus és modern szellemi felépítések összehangolására törekedett, nem ritkán olyanok is nagyra tartották, akik más ideológiai platformon álltak. Denis Diderot (1713–1784) azt mondta, ha valaki a maga képességeit összehasonlítja az övével, hajlik rá, hogy könyvei hátrahagyásával egy elhagyatott szegletbe vonuljon meghalni. A nagy logikus, Friedrich Ludwig Gottlob Frege (1848–1925) a gondolatcsírák pazar bőségét bámulta a műveiben. Savoyai Jenőt (1663–1736) annyira elkápráztatta Leibniz filozófiája, hogy amint erről tréfás túlzással az akkor még katolikus, később muzulmán Claude Alexandre de Bonneval (1675–1747) gróf a levelében beszámol, úgy őrzi Leibniz egy írását, mint nápolyi papok Szent Januáriusz (†305) vérét, akik egy csókot engednek, aztán gyorsan visszazárják a ládikába. És hogy mi is ez az írás? Leibniz filozófiájának kvintesszenciája, a nagy művei sorában az egyik legkésőbbi, az 1714-ben kiadott Monadológia, melyet éppen Savoyai Jenő Bécsben tett felkérésére írt, aki el volt ragadtatva az 1710-ben megjelent Théodicée-től, hosszabb címén az Essais de Théodicée sur la Bonté de Dieu, la Liberté de l´Homme et l’Original du Mal, Természetes teológiai értekezések az isteni jóságról, az ember szabadságáról és a rossz eredetéről című munkájától. (A théodicée szó mint „istenigazolás” magától a szerzőtől származik Turay Alfréd 1990-es megállapítása alapján.) Abban a módban, ahogy Leibniz az anyagi testeket éppúgy, mint a világot a maguk sajátos módján megjelenítő, egymásból le nem vezető szubsztanciákat hierarchikusan egyre kisebb elemek, végső soron a legkisebbek, a monászok építik fel, a matematikusi vénájú filozófusok nyilván azonnal felfedezik Leibniz és kora infinitezimális felfogását, a „végtelen kicsinyek” világának szédítő, beláthatatlan egymásra épülését, melyben ő végállomást pillant meg. Arra a kérdésre, hogy az egymással nem elegyedő szubsztanciák, mint legnevezetesebben test (mint elsősorban kiterjedés) és lélek (vagy általánosabban tudat) milyen módon képesek egymással kapcsolatba lépni, sok filozófus képzeletét megmozgatta. A „szubsztancia” fogalmán az „akcióra képes létezőt” érti, és ha ezzel nem hozta volna közelebb szívünkhöz, kitetszik, hogy John Duns Scotus (1266–1308) elképzelését helyezi át a nem kevésbé homályos újkori filozófia nyelvezetébe. Duns Scotus szerint szubsztancia az a nem mennyiségi tulajdonság, mely meghatározza a létezők egyediségét. Ezt a vonást szép latin szóval is illetik: haecceitas, magyarul „haecceitás” vagy „ezség”. És mivel Leibniz is tartja magát ahhoz (1695-ben A természet új rendszerében), hogy a szubsztanciák nem bírnak valóságos befolyással egymásra, ő is felállítja azok együttműködésére a maga magyarázatát. Az oratoriánus Nicolas Malebranche (1638–1715) azon a nézeten van, hogy a mindenre kiterjedő Gondviselés permanens (bár kifürkészhetetlen) kapcsolatot teremt a szubsztanciák között. Ezt az érzékeny Leibniz elveti, mert kitapintja benne Baruch Spinoza (1632–1677) „veszedelmes” panteizmusát. Helyette okkazionalista véleményt hangoztat: az eleve elrendelt harmóniát, a harmonia praestabilitát. Az isteni bölcsesség úgy harmonizálja a szubsztanciák, például a test és a lélek működését, mint ahogy az ugyanarra a rúdra függesztett két inga egymásra hangolódik. (Az órakereskedő fogása, mellyel azt sugallja, ingaórái hajszálpontosak, hiszen lám, mind ugyanazt az időt mutatja – csakhogy azért, mert a közös rúd hangolja egybe az ingák lengését.) Isten létezését Canterburyi Szent Anzelm (1033–1109), „a skolasztika atyja” nagy hullámokat vetett, 1078-ban felállított ontológiai istenérvére alapozva vezeti le lépésről lépésre. Ennek megfelelően egy ens perfectissimum, tökéletes lény tökéletessége csorbát szenvedne, ha nem bírna a létezés tulajdonságával, tehát létezik. Csűrjük-csavarjuk, töltsük ki aprólékos részletekkel a mondat két felét, nem szabadulunk attól a kisiklástól, hogy az érv vallói a létezést tulajdonságként kezelik (noha a mai napig kérdéses, kezelhető-e egyáltalán akárhogy is). De ugyanúgy felkarolja a kozmologikus istenérvet is: minden jelenségnek van egy kiváltó oka, láncolatosan egymásba fűzve, de magának a mindenségnek az oka valahol kívül kell essék, és ez a végső ok maga Isten. Itt az „ok” fogalmának tisztázatlansága vezet a spekulatív tanhoz. Leibniz azt vallja, mondhatni ez a legnagyobb feltűnést kiváltó filozófiai nézete, hogy minden lehetséges világ legjobbikában élünk, mert ezt választotta ki számunkra Isten. Minden egyéb ellene mondana az ens perfectissimum maximális jóságának. Itt a „lehetséges” szó jelentésével támadnak nehézségek, amelyek alapvetően kikezdik a tan érvényét.
Mondanunk sem kell, Leibniz provokatív nézetei ellenállást és gúnyt is kiváltottak. 1900-ban A Critical Exposition of the Philosophy of Leibniz, Leibniz filozófiájának kritikai bemutatása című könyvének előszavában Bertrand Russell (1872–1970) úgy találja, a Monadológia fantasztikus tündérmese, mely talán koherens, de teljességgel önkényes. Voltaire (1694–1778) felveti a kérdést: ha a vizelet egy cseppje monászok láncolata, hihető, hogy mindegyik visszatükrözi az univerzum teljességét? Legsúlyosabb csapását Leibnizre (akit kétségkívül sokat tanulmányozhatott) az 1759-ben megjelent Candide vagy Az optimista világnézet című utaztató szatirikus kisregényével mérte. Ennek 28. fejezetében (Mi történt Candide-dal, Kunigundával, Panglossal, Martinnal és a többivel?) különösen éles gúnnyal fogalmaz. Kemény Gábor 1924-ben megjelent fordításában:
– Én mindég az első nézetem mellett maradok, felelte Pangloss; végre is én filozófus vagyok, nem volna méltó hozzám, hogy ellenkezésbe jöjjek önmagammal; Leibniz ugyanis nem tévedhetett, az előre megállapitott harmónia a legszebb dolog a világon, ép oly szép, akár csak a nyers anyagi és a magasabbrendü szellemi lényeg összhangja.
Az optimizmus ádáz ellensége, Arthur Schopenhauer (1788–1850) fő műve, A világ mint akarat és képzet 1844-ben kiadott II. kötete 2. könyvének 46.fejezetében (Az élet semmissége és elszenvedése) így ír:
Leibniz Theodiceájának, az optimizmus e módszeres és bő kifejtésének nem tulajdonithatok ezen minőségében más érdemet, mint azt, hogy később a nagy Voltaire halhatatlan Candide-jára adott alkalmat, ami által persze Leibniznak annyiszor ismételt sántikáló kifogása a világ bajai ellen, hogy tudniillik némelykor a rossz a jót előidézi, ránézve váratlan bizonyitásra talált.
(A kötet nem jelent meg magyarul. A Candide 1924-es előszava idézi, feltehetőleg szintén Kemény fordításában.) Az 1818-ban elkészült I. kötet még „keményebben” fogalmaz a 2. könyv 59. fejezetében. A Tandori házaspár 1991-es fordítása szerint:
Mindazonáltal nem türtőztethetem magam ehelyt, s kimondom, hogy az optimizmus, már ahol nem csupán olyasak üres beszéde, kiknek szűk homloka mögött egyéb sincs, csak szó, szó, szó, szerintem nem egyszerűen abszurd, de egy ízig elvetemült gondolkodási mód, mely mintha csúfot űzni merészelne az emberiség kimondhatatlan szenvedéseiből.
Aligha kétséges, hogy e szavak a leghíresebb optimista ellen irányulnak. Mégis mond valamit az, hogy Leibniz 1663-as első filozófiai művének, az univerzálék valóságos létezését tagadó lutheránus nominalizmus hatása alatt álló bakkalaureátusi disszertációjának a címe De principio individui, Az individuáció (egyedivé válás) elvéről. Schopenhauer fő művének központi kategóriája ugyanis nem más, mint a principium individuationis, az egyediség alapelve – melynek fogalma természetesen Aquinói Szent Tamásig (1225–1274) megy vissza, és Schopenhauernél az egy és oszthatatlan akarat kifürkészhetetlen hajlamát jelenti a világ sokszínűségében megjelenésére. A névadás számtalan lehetséges okának sorából a Leibniz előtt tett főhajtást kizárhatjuk. Mindössze annyit mondhatunk, hogy Leibniz még akkor sem könnyen megkerülhető, ha minden igyekezetünkkel erre törekszünk.
Ezt olvastad?
További cikkek
„Olvassanak el mindent, hallgassanak meg minden véleményt, amit csak lehet!” – Interjú Vonyó József történésszel. 2. rész
Két héttel ezelőtt közöltük Vonyó Józseffel készített interjúnk első részét, amelyben főként az oktatás és a pályaválasztás motivációja, körülményei kerültek a középpontba. Most folytatjuk a kutatómunkával, politikai szerepvállalással, településtörténet-írással kapcsolatos […]
Zubovits Fedor, az igazmondó Háry János – interjú Kazareczki Noémivel
Hogyan lehet egy Háry Jánoshoz hasonlított ember mégis igazmondó? Krúdy Gyula minden bizonnyal tudta volna a választ, hiszen ő volt az, aki Zubovits Fedort ezzel a kifejezéssel írta le. A […]
„Egy szavamat se higgyék!” – Interjú Vonyó József történésszel. 1. rész
Vonyó József történész, nyugalmazott egyetemi oktató, az MTA doktora. Fő kutatási területei a 20. századi magyar politika- és társadalomtörténet, illetve a helytörténetírás módszertana. A Pécsi Tudományegyetem professzoraként számos hallgató útját […]
Előző cikk
Amiről beszélni nem lehet – A Soha, sehol, senkinek című filmről
A Soha, sehol, senkinek című film Téglásy Ferenc 1988-ban bemutatott alkotása, mely igen nagy sikert aratott nemcsak a hazai, de a nemzetközi filmiparban is, hiszen elnyerte többek között a Tórinói […]













